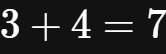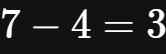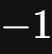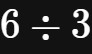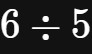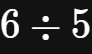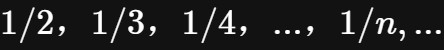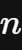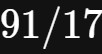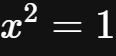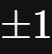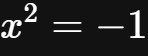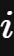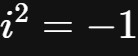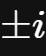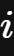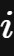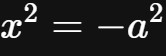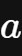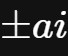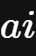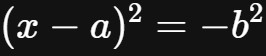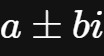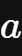一文读懂什么是数域,学习数学远比你想的简单|数学那点事
数学,能够决定一个学生高考的结果,甚至间接影响着人生的走向。
万千的中学生,每天都面对着和数学的战争。以高中数学为例,基础的数学公式有127个,衍生公式超过200个,基本的定理有162个,衍生出的推论超过300个,而大大小小的知识点和考点,更是可以细分到500个以上……
为什么有些学生,可以轻轻松松在高考数学中拿到140分,而有些学生,却在90分的及格线上挣扎?
这篇文章,也许能真正帮你开启正确学习数学的大门。
当我们在学数学的时候,我们在学什么?
如果要用一个词准确描述数学,你脑海中会跳出哪个词?
上面这些问题,就蕴含着数学学习的终极奥义。读完此文,你就会有答案。
已经有证据表明,在10万年以前,人类的祖先已经能够用计数的方法进行简单的加减运算。大家要知道,古人类绝不是酒足饭饱之后,为了娱乐而创造数学。数学,在那个渔猎时代,是人类与生活艰难的抗争中,被迫创造出来。数学,就像火与石器,成为早期人类生存的依仗。
而数域(Number Field)是数学发展的起源,数域的演化过程,处处体现出人类祖先和这个世界抗争的无奈,就让我们一起,重新感受这段艰辛的历程从中寻找学习数学的答案。
整数(Integers)
整数包含了正整数、零和负整数。其中,正整数是最早被人类所创造的。
正整数(Positive Integers)
有可靠的证据显示,正整数可能在数万年前,就已经能够被人类的祖先熟练使用了。大家可能要问,为什么这么早?!
因为当时的生活,真的太难了。
当放牧这件事开始出现的时候,牛羊就成为一个家庭最重要的资产之一,为了能够数得清楚牛羊的数量,或者为了准确描述来偷袭牛羊的狼群的规模,人类发明了正整数这个工具。
而能否熟练掌握正整数,已经成为当时人类能否好好活下去的重要技能之一。比如部落之间的战争,你需要清楚敌人的数量,并且准确把这个数量告诉你的族人,这关乎着战斗的胜负,也关乎着部落的命运。
零(Zero)
很不幸,如果一个家庭的牛羊,一夜之间被狼群全部咬死了,那么人们该怎么传递这样一个悲伤的消息呢?这时候,数字0诞生了。
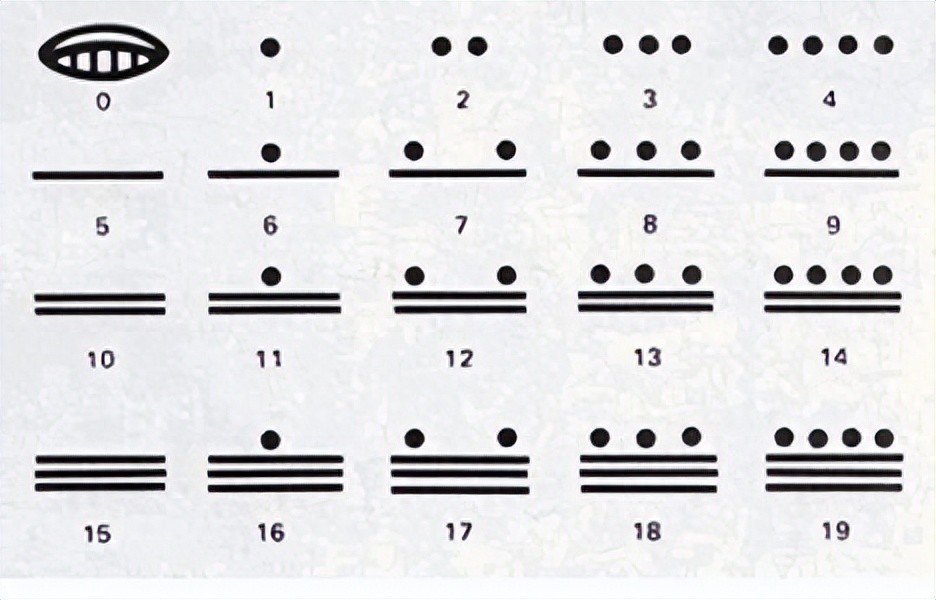
古玛雅的数字表示系统(图片来自网络)
在人类的书写系统尚未诞生之前,0就已经被创造了出来,人类祖先为了记录某一个可量化的事件消失殆尽(比如牛羊全部死亡,或者敌对部落的敌人被全部清除掉),就在洞穴的墙壁上,刻一个圆圈,这就成了0的由来。
正整数和零用来描绘自然界真实存在的数量(物品的数量或者人的数量),所以我们把它们统称为自然数(Nature Numbers)。
读到这里,有没有发现,当你知道了自然数这个名字的由来后,再遇到“自然数包含0吗?”这样的问题时,你再也不会出错了。
负整数(Negative Integers)
随着正整数和零被越来越多的人在生活中使用着,人类渐渐地可以熟练地掌握整数之间的加法和减法,计算
或
已经成为非常简单的事情。
可是人们发现,当需要计算
时,就遇到了障碍。这是人类使用数学工具的过程中,第一次遇到瓶颈。
为了能够让所有整数之间的减法都顺利的进行,负整数被定义了出来。此时
就可以流畅地计算出结果,即
。
负数无法用来描述自然界的数量,所以它不属于自然数,因为没有任何东西的数量是负的。但是负数可以描绘人类社会的关系:假如一个人一贫如洗,还欠了银行的钱,那么我们可以说这个人的资产是一个负数。

汉朝时期的《九章算术》已有对负数概念的记载(图片来自网络)
正整数、零和负整数,就构成了整数这个集合(集合这个工具的意义和性质,我们将在下一篇讲述)。有了整数,人们终于可以自由地去计算任意整数之间的加法、减法和乘法运算了。
但是,新的问题又出现了。
分数(Fractions)和小数(decimals)
当人类驯化了谷子、小麦和水稻这些农作物的时候,农耕时代开启了。如果一个农民在秋天只收获了1袋小米,却要平均分给3个家庭,该怎么去计算呢?
分数(Fractions)
现在,我们当然知道,这就是简单的除法,可是在分数没有被创造之前,人类在进行整数的除法运算时,时常会困惑,因为固然
这样的问题可以在整数范围内求解,但是
就不能进行了。这是人类使用数学工具的过程中,第二次遇到瓶颈。
为了让整数的除法也可以顺利进行下去,人类创造了分数。例如,
这个分数,就可以快速表示出除法关系
的结果。
假如,将所有的整数按照顺序放置在一条直线上,那么任意两个相邻的整数之间,都存在着间隔,而在每一个间隔内,又都可以放置无数个分数。
例如在整数0和1之间,可以放得下
,随着
的增加,你可以找到无穷多个位于0和1之间的分数(当然,还有
等更多的分数我们尚未提及)。
分数的创造,是数字发展过程中一个值得纪念的里程碑,至此,加减乘除四则运算,就具有了封闭性(即所有整数和分数组成的集合进行四则运算后的结果,依然位于这个集合内),简单来说,这些。
但是分数这种表现形式,依然存在着弊端,而其中最显著的一个问题是“不够直观”。例如, 91/17 这个分数,我们很难一眼看出它的值位于哪两个整数之间。
小数(Decimals)
为了改善分数的直观性,小数点这个新的工具就诞生了。借助小数点,分数和小数之间可以进行灵活的相互转化。
例如上述的分数
,可以转换为 5.352941... ,这样我们一眼就可以看出它的值介于5和6之间,这在对精确性要求不高的数学应用中,就显得极为方便。
分数到小数的转化过程中,人们发现了一个清晰的规律:所有的分数都可以转化为有尽小数(finite decimals)和循环小数(repeating decimals)。
人类是一种懒惰的动物,更倾向于喜欢有规律可循的事物。整数、有尽小数和循环小数的规律性令人愉悦,因为上述三种数字,均可以表示为某两个整数之比的形式(整数可看作其自身与1的比),所以人们将上述3种数字统称为有理数(rational numbers)。
但是,很不幸,随着数学的发展,人们发现了有一类小数,不但无限,且不循环,即无限不循环小数(infinte non-repeating decimals),例如圆周率
和自然常数
。即使全世界运行速度最快的超级计算机无休止地工作,也无法找到这类小数的尽头,人们把这种无法用任何两个整数之比的形式表示的小数命名为无理数(irrational numbers)。
当我们把整数、分数和无理数,都放置在一条直线上时,就发现,任意两个有理数之间,都可以安置无穷多个无理数,而无理数,恰好能填满任意两个有理数之间的间隔。
至此,我们得到了一条完整的直线,直线上任意一个点,均对应着一个有理数或无理数,我们将这样的一条想象出的直线称为数轴(number axis)。
实数(Real Numbers)与复数(Complex Numbers)
在很长一段时间,人们一度认为有理数和无理数,就是这个世界所有的数字了,人们开始变得不思进取,对于数字的探寻也告一段落,转而开始大量研究数字之间的关系。
随着研究的深入,函数和方程开始被广泛的应用,而对于含有未知数的方程求解成为了日常生产和工作中无法被忽视的技巧。
在求解方程的根的过程中,人们发现了一元二次方程的判别式(discriminant)、韦达定理(Vieta's Theorem)、余项定理(Remainder Theorem)等等众多的工具来辅助计算。
现在,只要7年级以上的同学,都可以一眼看出
这个方程存在两个解,即
。但是,如果你的眼前出现的方程是
,那么求根的过程便戛然而止,因为没有任意一个已知的数字,可以满足此等式。
这是人类使用数学工具的过程中,第三次遇到瓶颈。
为了能够让
得以运算,虚数单位
被人为地定义了出来。
我们定义
,那么上述方程就可以求得2个根
。
虚数(imaginary numbers)是人为构想出来的数字,其因此得名;和虚数相对应的,便是有理数和无理数,我们称其为实数(real numbers)。
被称为虚数单位(imaginary unit)。
借助虚数单位
,一个简单方程
(其中
是实数)可以求出2个虚数根
。
我们将形如
这样一个实数与虚数单位的乘统称为虚数。
更一般地,方程
可以求出2个根
。
我们将形如
(其中
和
均为实数)的组合称为复数(complex number),其中
称为复数的实部(real part),
称为复数的虚部(imaginary part)。
复数终于完成了数域(number field)最后一块拼图。数域,可以简单被理解为数字与运算关系组成的一套自洽的系统,在这个系统内,除了小心0不能作为除法的除数以外,我们几乎可以肆无忌惮地去完成所有的混合运算。
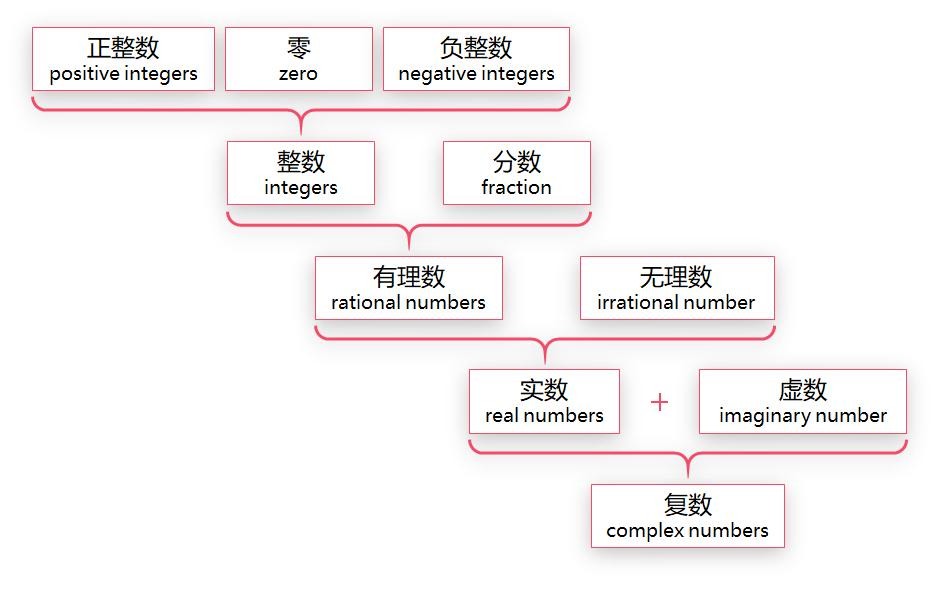
了解了数域发展的过程后,数域的结构就变得一目了然
结合数字发展的历史,数域的知识,已经能够清晰地看出知识的框架结构了。
总结
当我们试着回顾数域的核心发展历程以及理解了驱动数域发展的内在动力之后,我们清晰地发现,基础数学完全是为了服务于人类的生产与生活而被创立和研究的。另一个更加直观的例子,是几何学的建立和发展。古代的统治者和农民需要想办法去丈量土地,渐渐总结出平面图形的面积计算公式;古代的家庭需要计算他们的粮仓能够存储多少的粮食,因此体积的计算就成为了不得不去思考的事情。
所以我们现在终于可以自信地回答文章开头的那个问题了。当我们在学习数学的时候,我们在学习什么?其实,我们就是在学习,如何使用工具,就是这么简单。
所以,无论是整数、分数、复数这样的数字,还是各种各样看似繁杂的公式与定理,其实都只是人们创造或发现的工具,这些工具,帮助人们用更简单的方式,去感知和量化这个世界。
那么试着回忆一下,当我们去学习使用一种工具的时候,应该经历哪些步骤呢?
回忆我们使用筷子的经历,不难想见:
第一步,我们需要知道筷子用来做什么。答案显而易见,是为了方便我们饮食,这就是筷子作为一个工具的核心目的。顺着这个思路去反推,在筷子没有被发明之前,吃饭会遇到困扰吗?当然,我们的祖先直接用手抓食物,但是当你想捞起热汤里的肉块时,你显然不想把手伸进热汤里,而筷子作为手指的延申,不但可以让你吃饭时避免被烫伤,还能够让你的取食范围变得更大。所以,我们需要筷子这件工具。
相似地,在学习中,当我们遇到了一个新的数学工具,请先停下来思考,我们为什么需要它,它能帮助我们去解决怎样的问题,如果没有这个工具,那么我们是否会面临匮乏或局限。
第二步,我们需要知道如何正确地使用筷子。高效的筷子使用方法,是用一只手握着两根筷子,不是用两只手各握着一根筷子。
再次类比数学的学习,当我们认识了一个数学工具之后,要仔细研究它的使用方法和在解决问题中的局限性,因为每一个工具,必然有其限制条件,超越了某个条件,这个工具将失效。
第三步,我们需要多次的练习筷子的使用。当然,这种练习,是建立在上述两个步骤的基础上,然后,用不了多长时间,每个人都可以成为使用筷子的大师。
按照正确的方式去练习,是精通任何一个工具的必经之路,数学的学习也是一样,但再次之前,深入的思考及其的重要。
我是怪兽君,国际数学竞赛教练,高考数学146分,只做优质学习内容,欢迎关注。